Demagnetization

Loss of magnetization of permanent magnets due to high temperatures or inappropriate operating conditions.

Permanent magnet materials are characterized by their demagnetization curves, such as those found in Figures 1 and 2 for the material Neorem 712a. If the working point in any part of the permanent magnet exceeds the linear range, i.e. falls below the "knee" of the demagnetization curve, that part of the permanent magnet will be irreversibly demagnetized. This glossary post gives two examples of how demagnetization can occur and discusses how to ensure that your machine design is not at risk of demagnetization. For a more elaborate discussion of demagnetization issues of permanent magnets in electrical machines, please refer to [1].

1) Demagnetization due to high temperatures:

Figure 1 shows a fictive working line (in black) with two working points, with the upper operating at a temperature of 20°C and the lower at 100°C. Due to demagnetization, the demagnetization curve at 20°C will not recover to the initial upper red line, but will stay degenerated at the lower red line even after the temperature has decreased. As a consequence, the remanence flux density at 20°C will be reduced irreversibly from well above 1.3T to approximately 1.0T.

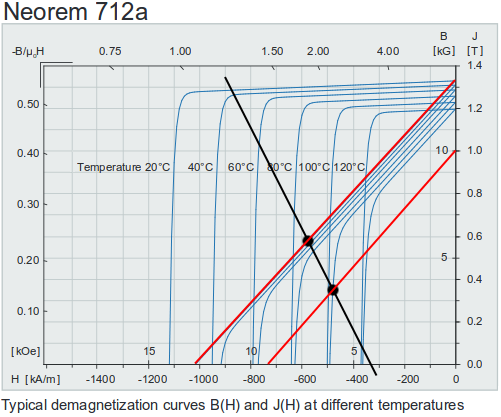
Fig. 1 Irreversible demagnetization due to a temperature increase from 20°C to 100°C.

2) Demagnetization due to inappropriate operating conditions:

Demagnetization of the permanent magnets must be considered for all possible operating conditions, especially those that move the working line of the machine towards the "knee" of the demagnetization curve. Those include short-circuits (single-phase, three-phase, and especially two-phase short-circuits, which are more common and more dangerous from a demagnetization point of view [1]), but also normal operating conditions such as line starting (before synchronization), field weakening (with negative d-axis current creating an opposing field), or short-time overload.

Figure 2 shows how a fictive working line (in black) that is subject to a change in operating conditions can move the working point to the left below the "knee" of the demagnetization curve. The new demagnetization curve at 60°C (red line) is irreversibly reduced, as is the remanence flux density which drops from almost 1.3T to below 1.1T.

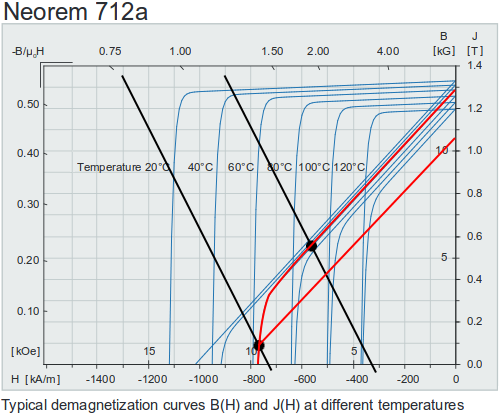
Fig. 2 Irreversible demagnetization due to a short-circuit at 60°C.

In Emetor, the demagnetization curve is currently strictly linear and described by the remanence flux density and relative permeability. As a consequence, simulations in Emetor are at the moment not subject to demagnetization. Therefore, you should make a habit of always checking your simulation results for possible risk of demagnetization. With this simple check you should be on the safe side:

1. Check the Emetor output for the minimum permanent magnet flux density (compare with the magnetic field plot in order to see which parts of your permanent magnets are at risk).
2. Check that this value is above the "knee" of the demagnetization curve. The demagnetization curve is available from the data sheet of the respective permanent magnet material in the electrical steel database.
3. If your machine design is at risk of demagnetization, you could consider changing the permanent magnet material, increasing the magnet thickness or airgap thickness, or reducing the maximum temperature that the permanent magnet is exposed to.

In practice, one indication that the permanent magnets of your machine have been partly demagnetized is an increase in current demand. By running an open-circuit test, you can verify if the induced voltage (back-EMF) has been reduced, which indicates that you indeed have an issue with demagnetization. You should also keep in mind that the demagnetization curves from the manufacturers are typical values, with tolerances of up to ±10%.

References:
[1] Sami Ruohu, Demagnetisation of Permanent Magnets in Electrical Machines, Helsinki University of Technology, 2006

Read about another glossary term