Average conductor length
Average length of a conductor including the length of the end-winding.
The average conductor length is calculated as [1]: $$L+k_c\frac{2\pi r_w}{Q_s}$$ where $L$ is the machine length, $r_w$ is the average winding radius (distance from the centre of the machine to the middle of the slot), $Q_s$ is the number of stator slots, and $k_c$ is a parameter that takes into account the length of the end-winding. Depending on the type of winding, $k_c$ is calculated as:
| Distributed winding | $k_c$ = $\frac{\pi}{2} \cdot$ coil span in slot pitches |
| Single-layer concentrated winding | $k_c$ = 1.36 |
| Double-layer concentrated winding | $k_c$ = 0.93 |
According to the above equation, the average conductor length is always longer than the machine length. Fig. 1 shows an illustration of the average conductor length (red line) compared to the machine length (blue line) for a double-layer concentrated winding. In Emetor, the average conductor lenght is used to calculate the phase resistance, the conductor losses and the conductor mass.
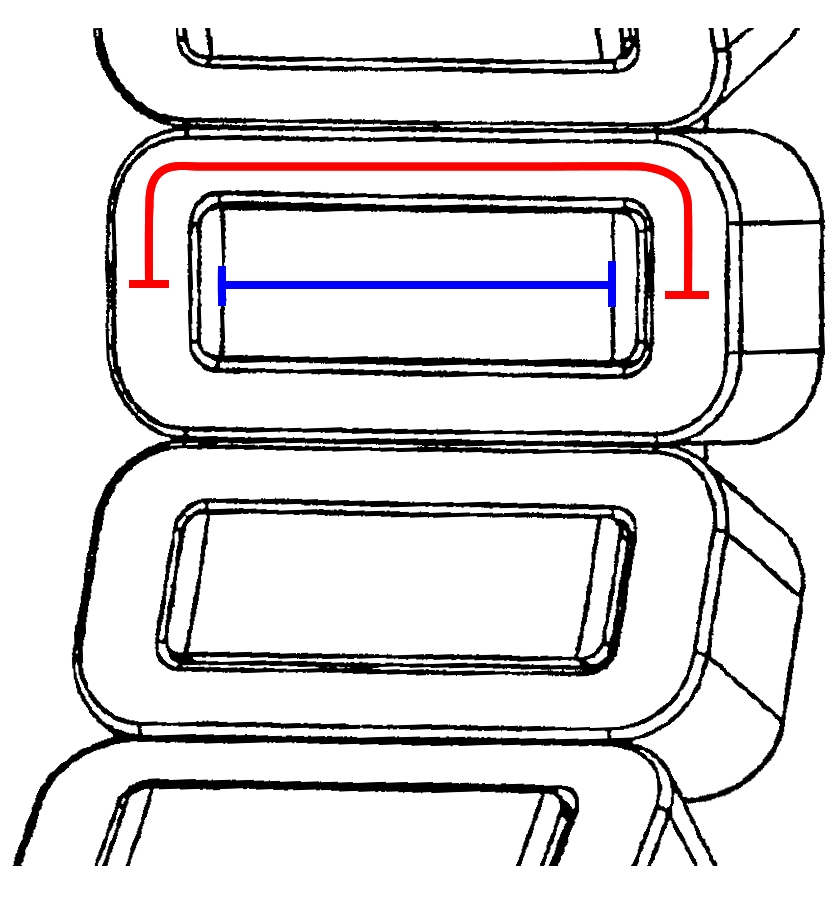
Fig. 1 Illustration of average conductor length (red) and active machine length (blue) on the example of a double-layer concentrated winding.
References:
[1] F. Magnussen, C. Sadarangani, "Winding factors and joule losses of permanent magnet machines with concentrated windings", Electric Machines and Drives Conference (IEMDC 2003), Vol. 1, pp. 333-339, 2003.
Read about another glossary term
